Computationally secure ciphers and pseudorandom number generators
A modern practical assumption is to build ciphers such that a successful attack is carried only if a computational hard problem is solved. Examples of such hard computational problems are:
- Solve a generic nonlinear bollean sim. equation set
- Factor large integers / find discrete logarithms
- Decode a random code / find shortest lattice vector
The method:
- Defines the ideal attacker behaviour
- Assume a given computational problem is hard
- Prove that any non ideal attacker solves the hard problem
Cryptographically Safe Pseudorandom Number Generators
A CSPRNG is a deterministic function $\text{PRNG: }\lbrace 0, 1\rbrace^\lambda \to \lbrace 0, 1\rbrace^{\lambda+l}$ whose output cannot be distinguished from an uniform random sampling of $\lbrace 0, 1\rbrace^{\lambda+l}$ in $O(poly(\lambda))$. $l$ is the CSPRNG stretch.
Building a CSPRNG "from scratch" is possible, but it is not the way they are commonly built (not efficient).
Practically built employing another building block: PseudoRandom Permutations (PRPs).
Modern PRPs are the outcome of public contests where cryptanalytic techniques provide ways (=poly(λ) tests) to detect biases in their outputs: good designs are immune. No formally proven PRP exists.
Block ciphers
Concrete PRPs go by the historical name of block ciphers.
Considered broken if, with less than $2^\lambda$ operations, they can be told apart from a PRP, e.g., via:
- Deriving the input corresponding to an output without the key
- Deriving the key identifying the PRP, or reducing the amount of plausible ones
- Identifying non-uniformities in their outputs
The key length $\lambda$ is chosen to be large enough so that computing $2^\lambda$ guesses is not practically feasible.
Advanced Encryption Standard (AES) is the most widle used block cipher. Data Encryption Algorithm (DEA or DES) was the previus legacy standard.
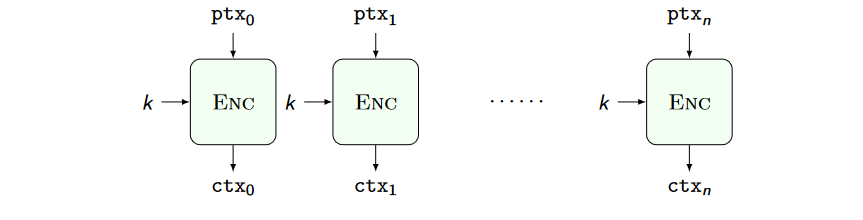
Electronic CodeBook (ECB)
Is the first attempt to encrypt using PRPs.
It is ok to encrypt a plaintext which lenght is less that the block size.
In order to extend to longer plaintexts we could use multiple blocks and split the plaintext:
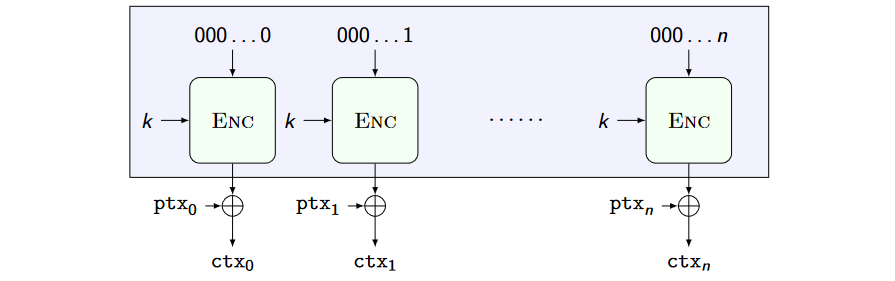
Counter (CTR) mode
The boxed construction is provably a PRNG if Enc is a PRP.