Skip to main content

Bayesian Networks

Bayesian Networks are data structure that represents the dependencies among random variables:

  • Directed graph
  • Each node represents a random variable
  • A direct edge from $X$ to $Y$ means $X$ is a parent of $Y$
  • Each node $X$ has probability distribution $P( X | Parents(X) )$

For example:

  • "Rain" ($R$) is independent and it has the probabilities $P(R)=\lang 0.7, 0.2, 0.1 \rang$
  • "Mainteance" ($M$) depends only on $R$, so:
    • $P(M|R=\text{none})=\lang 0.4,0.6 \rang$
    • $P(M|R=\text{light})=\lang 0.2,0.8 \rang$
    • $P(M|R=\text{heavy})=\lang 0.1,0.9 \rang$
  • "Train" ($T$) depends both on $M$ and on $R$, resulting in the following probabilities:
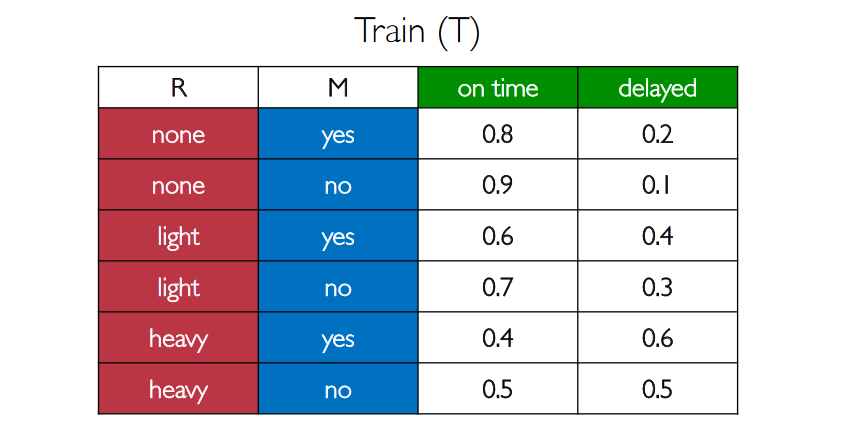
  • "Appointment" ($A$) depends only on $T$:
    • $P(A|T=\text{on time})=\lang 0.9, 0.1 \rang$
    • $P(A|T=\text{delayed})=\lang 0.6, 0.4 \rang$

Computing join probabilities

From a bayesian network we can easily compute some interesting probabilities which are not explicitly defined.

In our example we could compute:

  • $P(R=\text{light} \land M=\text{no}) = P(R=\text{light})P(M=\text{no}|R=\text{light})$
  • $P(R=\text{light} \land M=\text{no} \land T=\text{delayed})=P(R=\text{light})P(R=\text{light} | M=\text{no})P(T=\text{delayed} | R=\text{light} ∧ M=\text{no})$
  • $P(R=\text{light} \land M=\text{no} \land T=\text{delayed} \land A=\text{missed})=P(R=\text{light})P(R=\text{light} | M=\text{no})P(T=\text{delayed} | R=\text{light} ∧ M=\text{no})P(A=\text{missed} | R=\text{light} ∧ M=\text{no} \land T=\text{delayed})$

Inference using bayesian networks

We want to compute distribution of a variable $X$ and we can observe an evidence variables $E$ for the event $e$. There is also a hidden variables $Y$ which is not observable. The goal is to compute $P(X | e)$.

In our example we may want to compute the probability to be on time but we do not know the probability of the train being delayed. However, we know there is light rain outside and there is no mainteance today.

We want to compute $P(A|R=\text{light} \land M=\text{no})$. Using marginalization: $$P(A|R=\text{light} \land M=\text{no}) = \alpha P(A \land R=\text{light} \land M=\text{no}) + \alpha [P(A \land R=\text{light} \land M=\text{no} \land T=\text{on time}) + P(A \land R=\text{light} \land M=\text{no} \land T=\text{delayed})]$$

\begin{split}    a & = b + c \ d = 4 \end{split}

Back to top