Example problems on uncertainty
Some example problems that could be asked in the exam:
- Given some knowledge about a problem, represent such knowledge as a Bayesian network
- Given a Bayesian network, specify what formula you need to compute a given probability
- Given a Bayesian network, compute the probability
Example
You are trying to design a Bayesian network to model the knowledge about the relation between the following series of variables:
- Exercise (with values Yes and No) $E$,
- Diet (with values Healthy and Unhealthy) $D$,
- HeartDisease (with values Yes and No) $HD$,
- BloodPressure (with values High and Low) $BP$,
- HeartBurn (with values Yes and No) $HB$,
- ChestPain (with values Yes and No) $CP$.
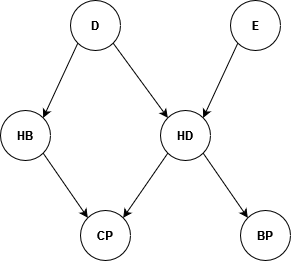
The physician describes the relation between these variables as follows: “Patients can experience chest pain if they have heartburn but also if they have a heart disease. Unhealthy diet influence possible heart diseases and heartburn. Regular exercise can limit problems of heart diseases. High blood pressure can be an effect of a heart disease.”
Exercise 1
Draw the Bayesian network that represent the physician knowledge.
Solution
Exercise 2
Suppose that I want to compute $P(BP=\text{High}, HD=\text{No}, E=\text{No}, D=\text{Yes})$. What computation should I perform to be able to compute it?
Solution
It is join probability so it can be computed using a "top-down" approach. I start from the independent variables and proceed in the network.
The result is $P(D=\text{Yes})P(E=\text{No})P(HD=\text{No}|D=\text{Yes}, E=\text{No})P(BP=\text{High}|HD=\text{No})$
Exercise 3
What if I did not know anything about the Diet?
Solution
If I knewwould nothingneed aboutto do the dietcomputation thenfor to be a valid bayesian networkthe all the probabilitiespossible shouldvalues beof expressedDiet independentlyand fromthen diet.I would need to normalize.
Exercise 4
What if I wanted to compute $P(BP=\text{High})$?
Solution
I could do inference by ennumeration to calculate the probability or use sampling for an approximation.
