Introduction
In this chapter we cover competitive environments, in which two or more agents have conflicting goals, giving rise to adversarial search problems.
We consider games with
- two players
- turn-taking
- zero sum
- perfect information
- deterministic and stochastic (they can include elements of chance)
- Zero sum: if a player wins (+1), the other player looses (–1); the sum is thus zero
- Perfect information: The agent has perfect information about the game state which is fully observable (like chess, unlike poker)
Games as Search Problems
Games can be formulated as search problems with an element of uncertainty due to the actions (moves) of the opponent
At each turn, a player must choose the action to play without the possibility to explore the whole state space and, in general, there is no sequence of actions that makes a player win independently of the actions of the opponent.
- Two players, MAX and MIN, that take turn. MAX moves first.
- Intial set up of the game (initial configuration of the board) is known.
- Function Action(s): Given a state s, returns the set of legal moves in s
- Function Result(s): Defines the state resulting from taking action a in state s
- Goal test: Given a state, returns true if the game is over
-
Utility(s,p): Returns the numerical value to player p in terminal state s (e.g., +1, 0, or –1)
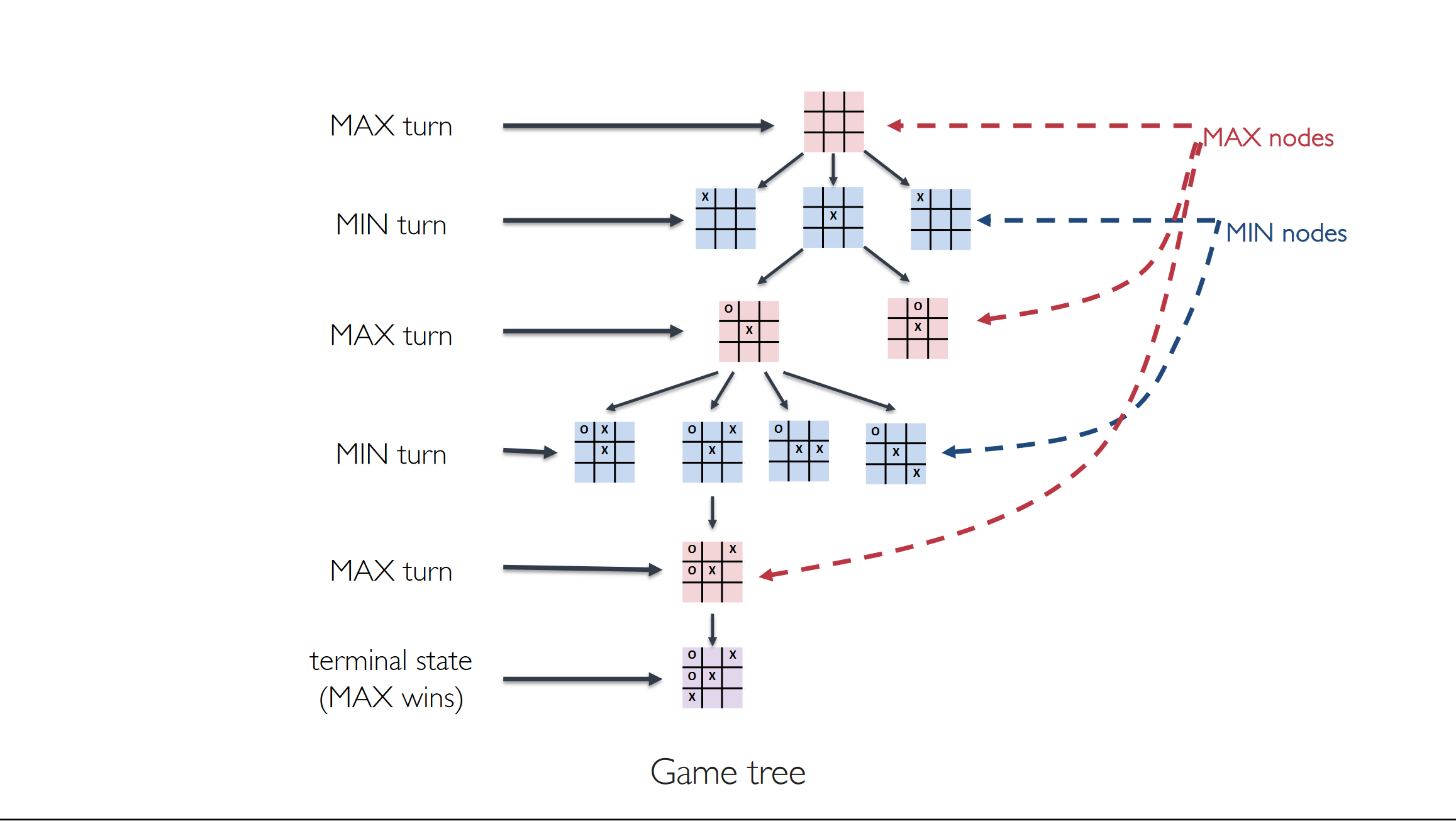 Solving the game corresponds to finding the best
action for MAX (or for MIN) in a given state.
Solving the game corresponds to finding the best
action for MAX (or for MIN) in a given state.
