Minimax search

MAX wants to find a sequence of actions leading to a win, but MIN has something to say about it. This means that MAX’s strategy must be a conditional plan—a contingent strategy specifying a response to each of MIN’s possible moves. 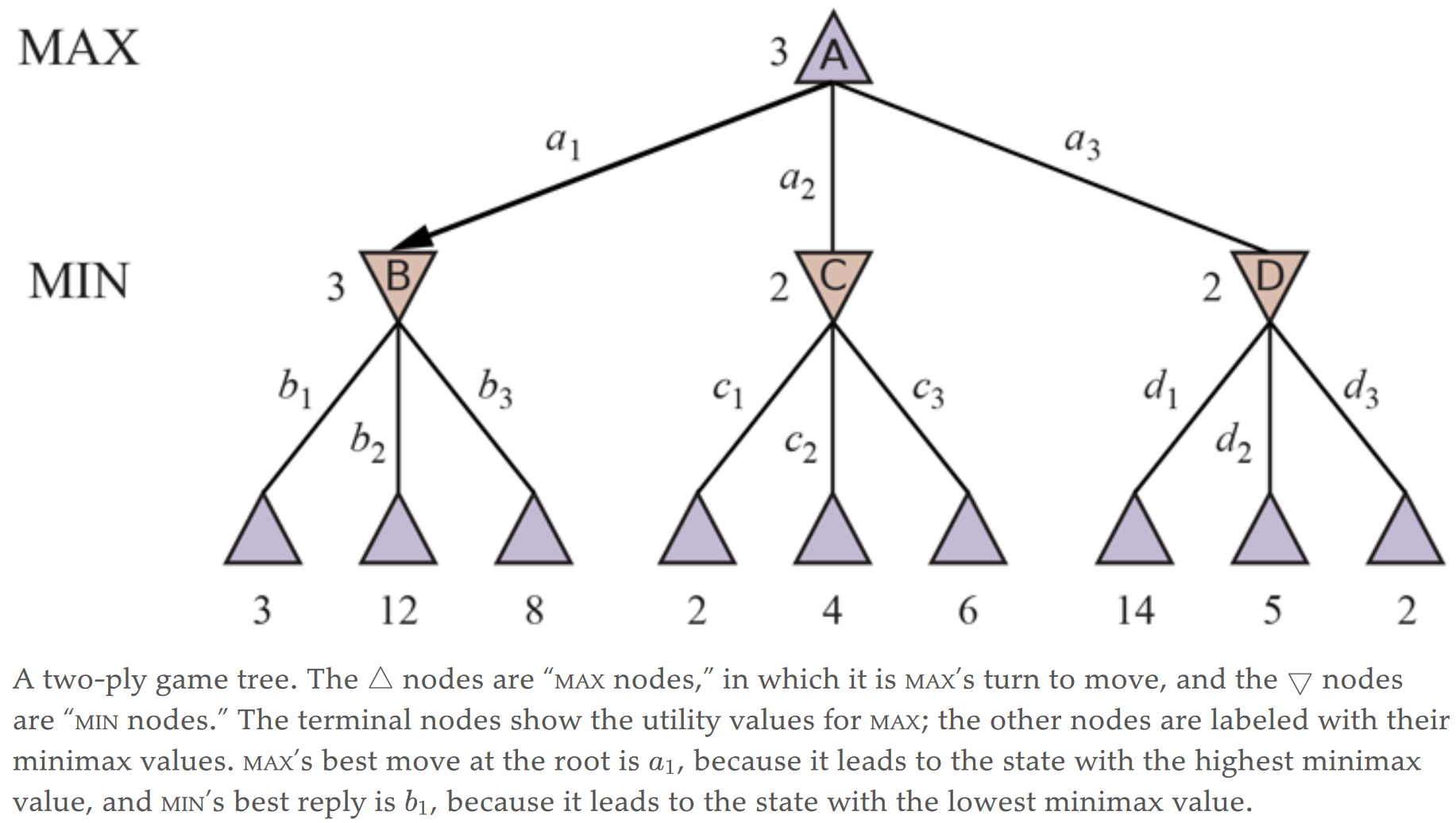Given a game tree, the optimal strategy can be determined by working out the minimax value of each state in the tree, which we write as MINIMAX(s). The minimax value is the utility (for MAX) of being in that state, assuming that both players play optimally from there to the end of the game.

Algorithm

It is a recursive algorithm that proceeds all the way down to the leaves of the tree and then backs up the minimax values through the tree as the recursion unwinds.

Complexity

The minimax algorithm performs a complete depth-first exploration of the game tree.

If the maximum depth of the tree is $m$ and there are $b$ legal moves at each point, then the time complexity of the minimax algorithm is $O(b^m)$. The space complexity is $O(bm)$ for an algorithm that generates all actions at once, or $O(m)$ for an algorithm that generates actions one at a time.

Evaluation

Minimax is optimal when using the utility function (when the entire game tree is built)