Theorem proving

Other than model checking entailment can be done by theorem proving—applying rules of inference directly to the sentences in our knowledge base to construct a proof of the desired sentence without consulting models. If the number of models is large but the length of the proof is short, then theorem proving can be more efficient than model checking.

1) Resolution

Resolution is similar to DPLL (when this is used to establish entailment): it starts from a CNF representation of the premises and the negation of the conclusion

Resolution applies (in all the possible ways) the resolution rule to the clauses (original ones and those derived by the previous applications of the resolution rule)

Suppose 𝐶1, 𝐶2 are clauses such that literal ℓ1 in 𝐶1 and literal ℓ2 in 𝐶2 are complementary (same propositional symbol with different sign), then clauses 𝐶1, 𝐶2 can be resolved into a new clause 𝐶 called resolvent C = (𝐶1 − {ℓ1}) ∪ (𝐶2 − {ℓ2})

Resolution properties

• Propositional resolution is an extremely powerful rule of inference for PL
• It works by refutation: to prove that KB ⊨ 𝛼 it proves that KB ∧ ¬𝛼 is unsatisfiable, namely it builds a refutation for KB ∧ ¬𝛼 by looking for the empty clause
• Using propositional resolution, it is possible to build a theorem prover that is sound and complete for PL
  • Resolution rule is sound
  • Theorem: resolvent 𝐶 is satisfiable if and only if clauses 𝐶1, 𝐶2 are simultaneously satisfiable
  • Since resolvent is smaller than parent clauses, resolution stops at some point
• Propositional resolution works on any set of sentences in clausal form (CNF)

2) Forward chaining

The forward-chaining algorithm determines if a single proposition symbol —the query—is entailed by a knowledge base of definite clauses. It begins from known facts (positive literals) in the knowledge base. If all the premises of an implication are known, then its conclusion is added to the set of known facts. For example, if $A$ and $B$ are known and $A \land B \to C$ is in the knowledge base then $C$ can be added. This process continues until the query q is added or until no further inferences can be made.

In an AND-OR graph multiple edges joined by an arc indicate a conjunction while without an arc a disjunction. For example:

Properties of forward chaining

Forward chaining is sound and complete for KBs composed of definite clauses

• Soundness: follows from soundness of Modus Ponens (easy to check)
• Completeness: the algorithm reaches a a fixed point from where no new atomic sentences can be derived

Forward chaining can only derive new positive literals (facts), it cannot derive new rules

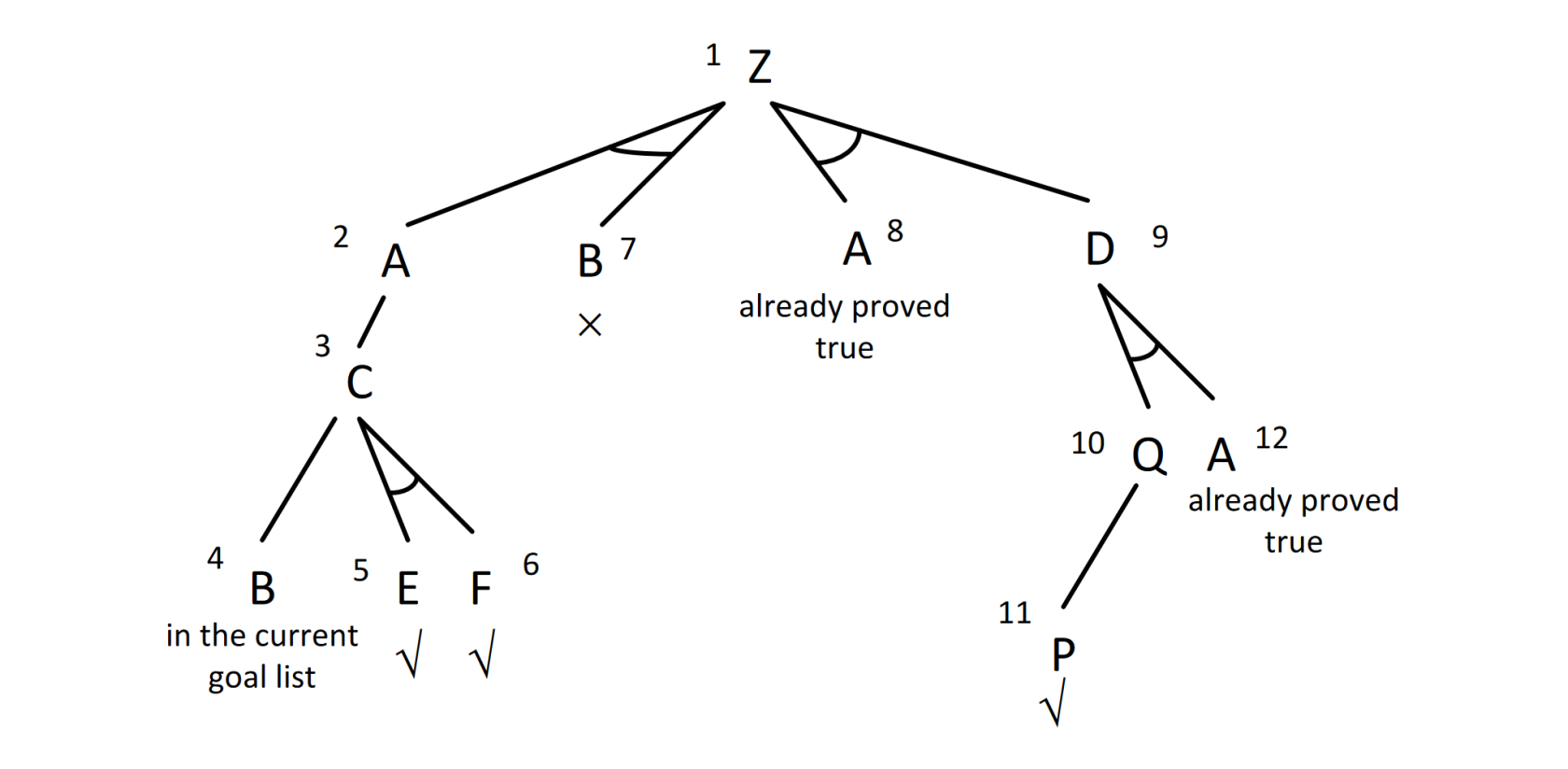
3) Backward chaining

The backward-chaining algorithm, as its name suggests, works backward from the query.

If the query $q$ is known to be true, then no work is needed. Otherwise, the algorithm finds those implications in the knowledge base whose conclusion is $q$. If all the premises of one of those implications can be proved true (by backward chaining), then $q$ is true.

In summary:

• Start from the goal (query) 𝑞, which is a positive literal
• To prove 𝑞, check if 𝑞 is already in the KB, otherwise prove all the premises of a rule concluding 𝑞
• Avoid loops: check if new subgoal is already on the goal stack
• Avoid repeated work: check if new subgoal has already been proved true, or has already failed

Backward chaining is sound and complete for KBs composed of definite clauses

Exam questions

2017 02 23 Q3 (7 points) Resolution

Consider the following knowledge base (KB) in propositional logic:

1. $A \to \lnot B$
2. $\lnot A \to \lnot B$
3. $A \lor B$

Prove, using resolution with the input resolution strategy, $A \to B$ can be derived from the KB.

Solution

The first step is to trasform in CNF and add the negation of the solution:

1. $\lnot A \lor \lnot B$
2. $A \lor \lnot B$
3. $A \lor B$
4. $\lnot (\lnot A \lor B)$, with De Morgan's rules:
   1. $A$
   2. $\lnot B$

Then apply resolution:

(1) $\lnot A \lor \lnot B$ and (3) $A \lor B$ become $B \lor \lnot B$ and $A \lor \lnot A$

We have reached a fixed point because any other application of the resolution rule with the input resolution strategy will not produce any new knowledge.

So, $A \to B$ cannot be derived from the KB using resolution with the input resolution strategy.

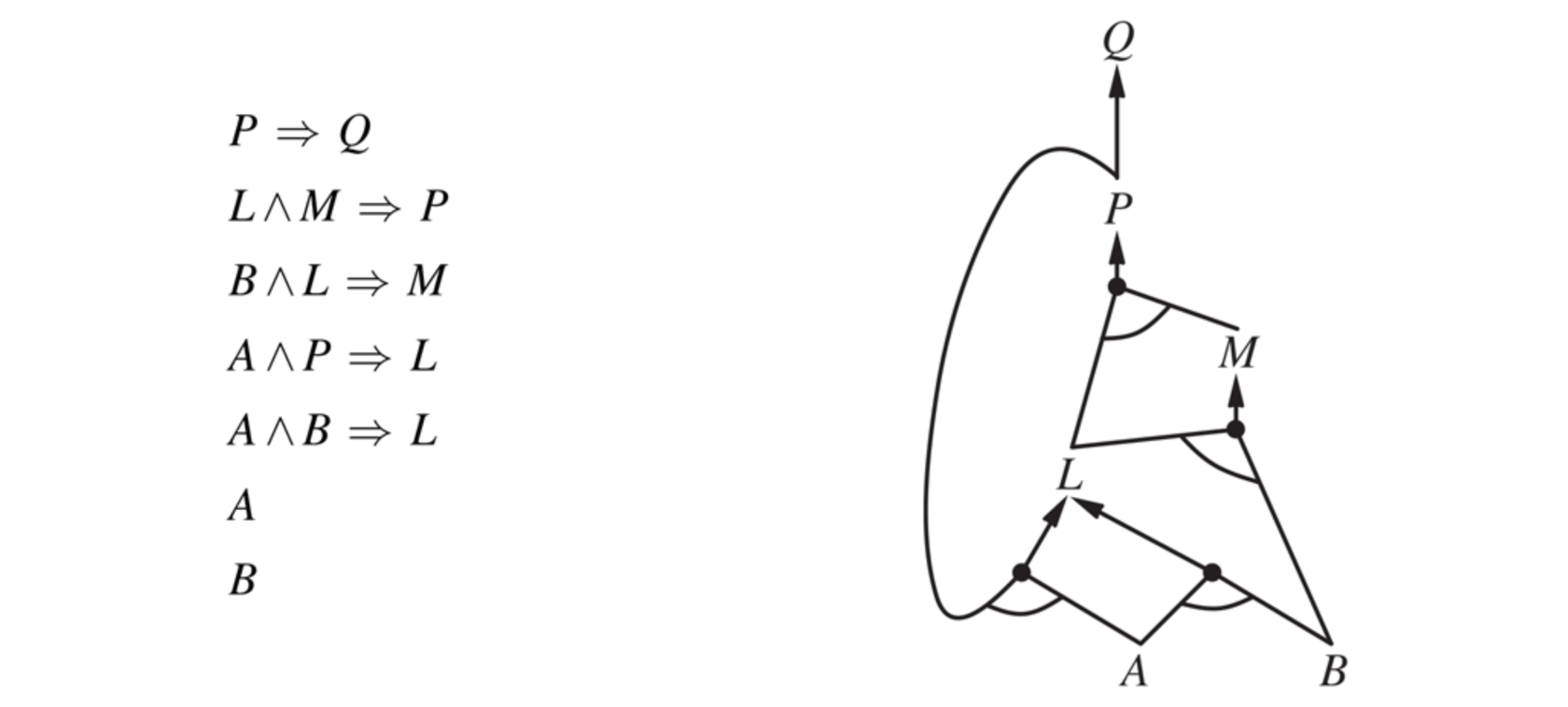
2017 02 03 Q3 (6 points) Backward chaining

Consider the following knowledge base (KB) in propositional logic:

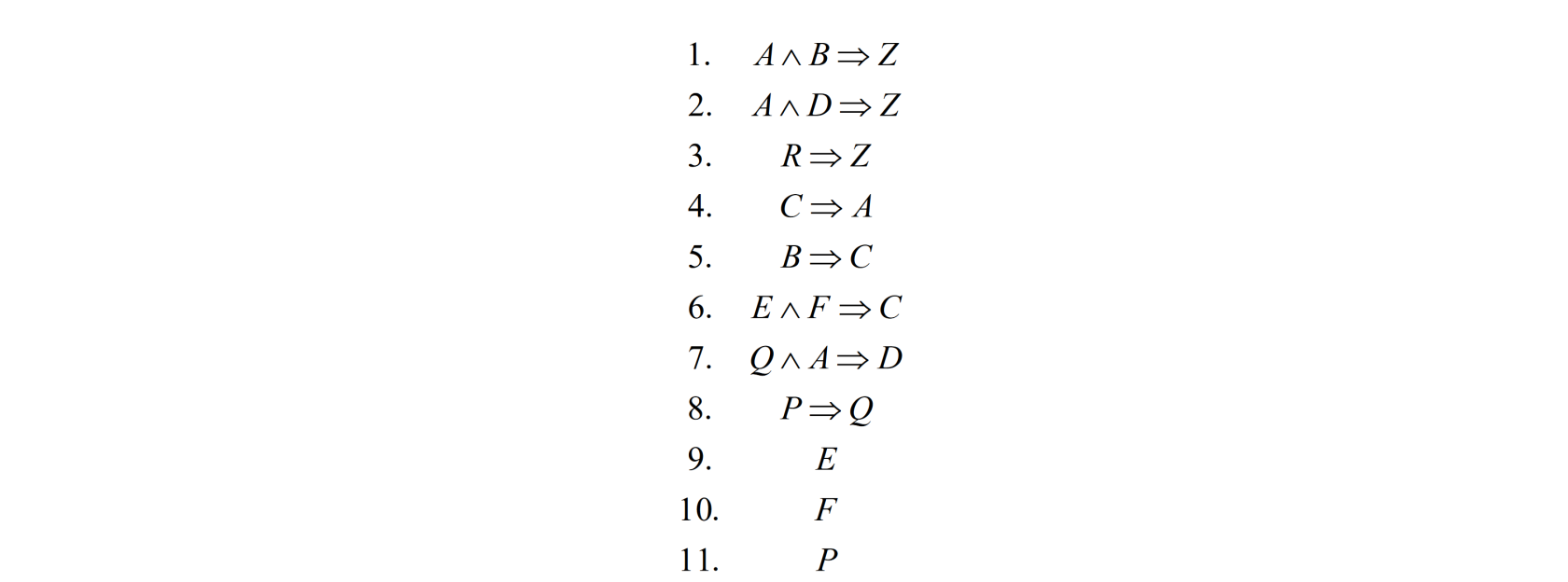
Prove, using backward chaining, if KB logically entails $Z$. Everything else being equal, apply the rules in the order given above. Report the generated tree and the order of expansion of its nodes.

Solution

Since $Z$ can be derived from KB using backward chaining, which is a sound inference procedure for propositional logic, then $Z$ is logically entailed by the KB.