Skip to main content

Backtracking Search for CSPs

Sometimes we can finish the constraint propagation process and still have variables with multiple possible values. In that case we have to search for a solution.

CSP is commutative: the order of application of any given set of actions does not matter. We need only consider a single variable at each node in the search tree.

With this restriction, the number of leaves is $d^n$, as we would hope (instead of $n! \cdot d^n$). At each level of the tree we do have to choose which variable we will deal with, but we never have to backtrack over that choice.

Backtracking repeatedly chooses an unassigned variable, and then tries all values in the domain of that variable in turn, trying to extend each one into a solution via a recursive call. If the call succeeds, the solution is returned, and if it fails, the assignment is restored to the previous state, and we try the next value. If no value works then we return failure.

Variable and value ordering

Which variable $X$ should be assigned next?

  • The current assignment could not bring to any solution, but we might need time to discover this
  • Choose the right variable in order to discover inconsistencies in the current assignment as soon as possible

Two heuristics:

  • minimum-remaining-values (MRV)
  • Degree

In what order should the values of $X$ be considered?

  • The current assignment could bring to a solution (could be part of a solution)
  • Choose the right value to assign to $X$ in order to reach the solution as quickly as possible

One heuristic:

  • Least-constraining-value

These aspects are domain-independent and made possibile by the factored representation of the state

minimum-remaining-values (MRV) heuristic

It also has been called the “most constrained variable” or “fail-first” heuristic, the latter because it picks a variable that is most likely to cause a failure soon, thereby pruning the search tree.

If some variable $X$ has no legal values left, the MRV heuristic will select $X$ and failure will be detected immediately—avoiding pointless searches through other variables. The MRV heuristic usually performs better than a random or static ordering, sometimes by orders of magnitude, although the results vary depending on the problem.

Degree heuristic

Choose the variable that is involved in the largest number of constraints with unassigned variables and it's used to break ties of the MRV heuristic.

Least-constraining-value heuristic

Choose the value that gives «more freedom» to the variables that are not yet assigned

Interleaving search and inference

We saw how AC-3 can reduce the domains of variables before we begin the search. But inference can be even more powerful during the course of a search: every time we make a choice of a value for a variable, we have a brand-new opportunity to infer new domain reductions on the neighboring variables.

One of the simplest forms of inference is called forward checking. Whenever a variable $X$ is assigned, the forward-checking process establishes arc consistency for it: for each unassigned variable $Y$ that is connected to $X$ by a constraint, delete from $Y$’s domain any value that is inconsistent with the value chosen for $X$.

A more powerful approach is to use AC-3, but instead of a queue of all arcs in the CSP, we start with only the arcs $(X_j, X_i)$ for all $X_j$ that are unassigned variables that are neighbors of $X_i$. From there, AC-3 does constraint propagation in the usual way, and if any variable has its domain reduced to the empty set, the call to AC-3 fails and we know to backtrack immediately.

Exam questions

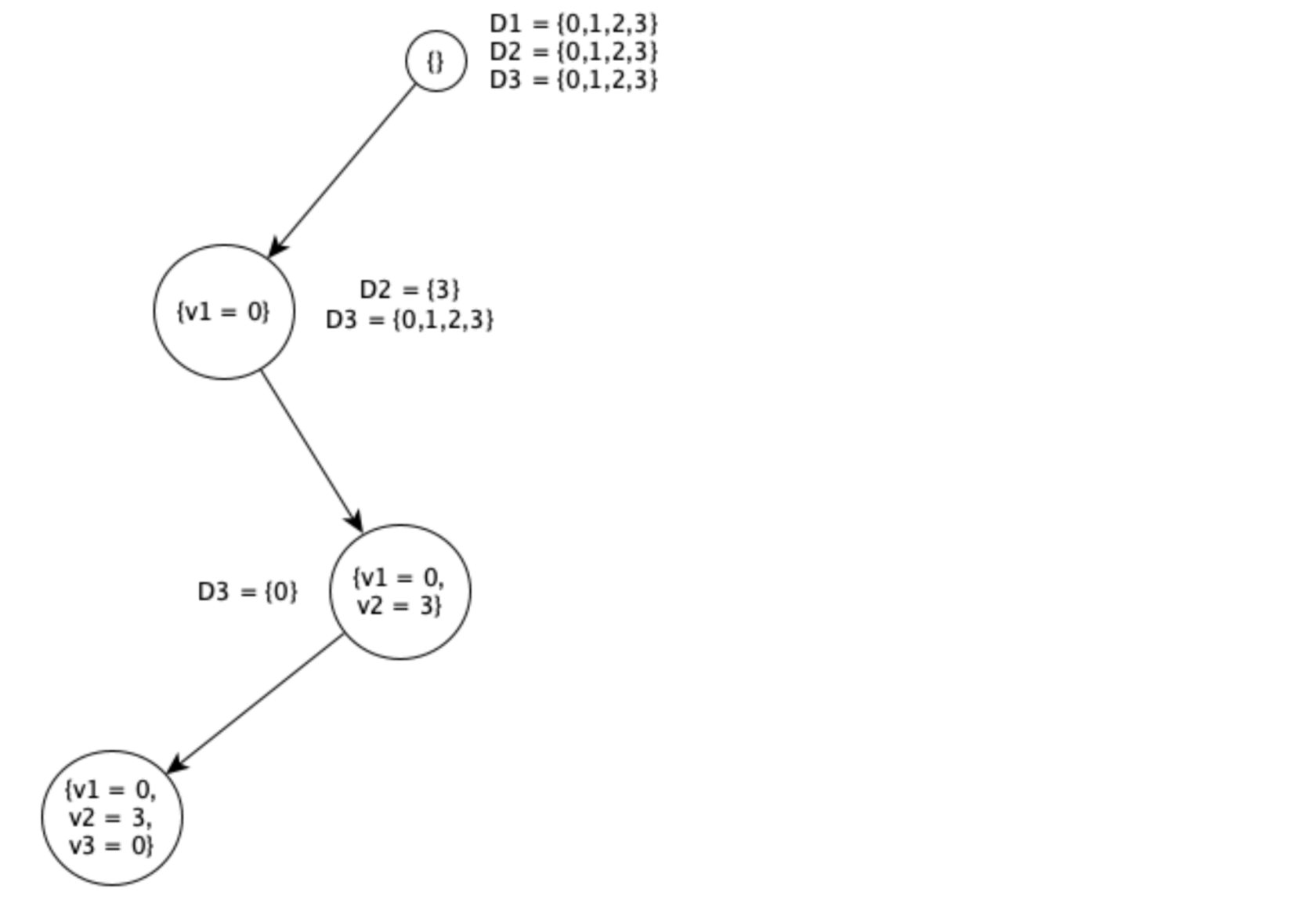
2020 01 20 Q2 (8 points)

Consider the following Constraint Satisfaction Problem (CSP):

  • variables: $v_1$, $v_2$, $v_3$
  • domains: $D_1$ = $D_2$ = $D_3$ = $\lbrace 0, 1, 2, 3, 4, 5 \rbrace$,
  • constraints: $v_1 + v_2 = 3$, $v_1 \le v_3$, $v_2 +v_3 \le 3$.

After AC-3 the domain have been restricted to: $D_1 = D_2 = D_3 = \lbrace 0, 1, 2, 3 \rbrace$..

  1. Then solve the above CSP using backtracking search with forward checking and Minimum Remaining Value (MRV) heuristic. Ties are broken lexicographically. Report the search tree and, for each node, the updated domains of unassigned variables. Report also the solution found.
Solution
  • Assign in lexicographical order $v_1 = 0$. The domain: $D_2 = \lbrace 3 \rbrace, D_3 = \lbrace 0,1,2,3 \rbrace$
  • $v_2 = 3$ because it is the most constrained variable. Then $D_3 = \lbrace 0 \rbrace$
  • $v_3 = 0$ because it is the only unassigned variable. We found a solution.

No Comments
Back to top