Monte Carlo Tree Search

The basic MCTS strategy does not use a heuristic evaluation function. Instead, the value of a state is estimated as the average utility over a number of simulations of complete games starting from the state. A simulation (also called a playout or rollout) chooses moves first for one player, than for the other, repeating until a terminal position is reached.

To get useful information from the playout we need a playout policy that biases the moves towards good ones. For Go and other games, playout policies have been successfully learned from self-play by using neural networks.

Need to balance exploration of states that have had few playouts, and exploitation of states that have done well in past playouts, to get a more accurate estimate of their value.

Montecarlo does that maintaining a search tree and growing it on each iteration of the following four steps:

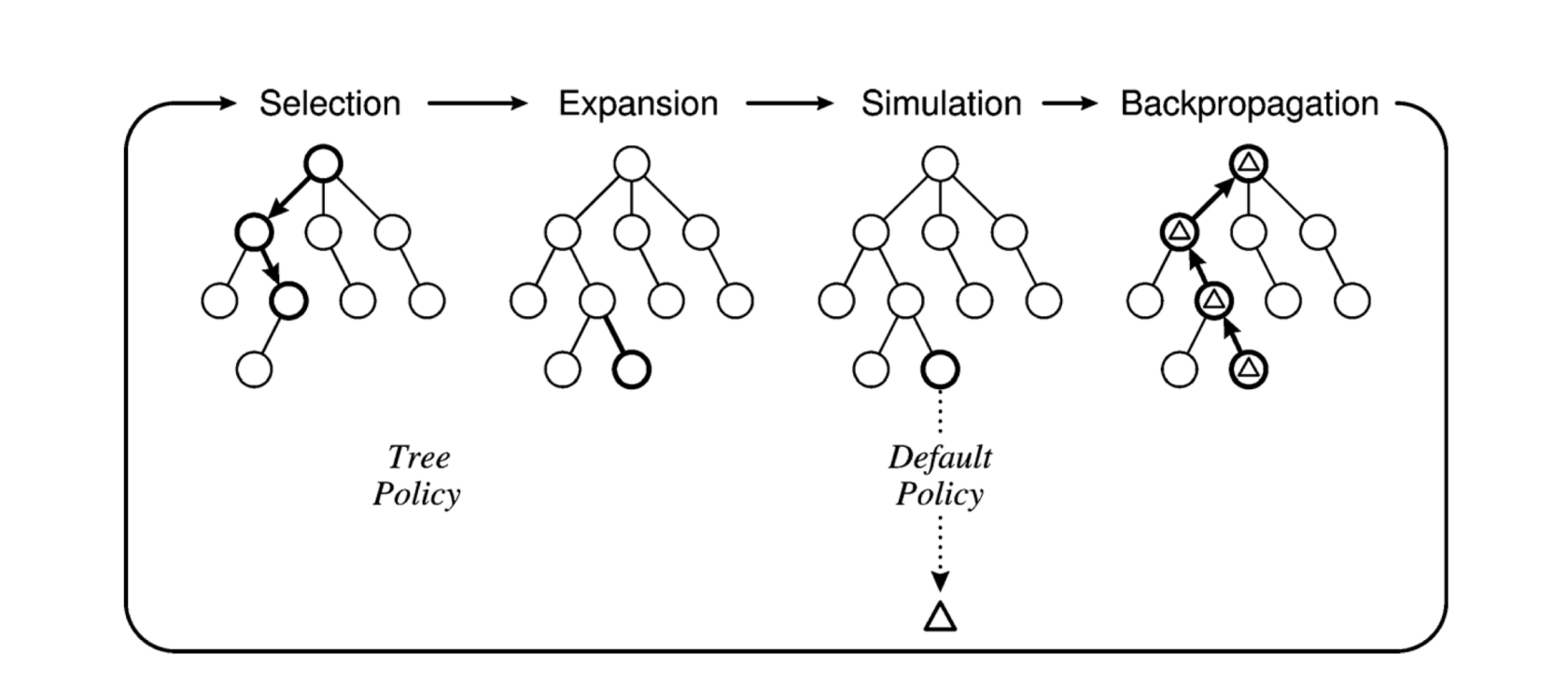
• Selection: It descends the game tree selecting successors using a selection policy until either a node with an unexpanded branch or a leaf is reached
• Expansion: We grow the search tree by generating a new child of the selected node.
• Simulation: We perform a playout from the newly generated child node, choosing moves for both players according to the playout policy. These moves are not recorded in the search tree.
• Backpropagation: We now use the result of the simulation to update all the search tree nodes going up to the root.

UCB1

UCB1(n) is a common solution to balance exploration and exploitation in MCTS. The node with the largest UCB1(n) is selected where UCB1(n) is: $$UCB1(n) = \frac{U(n)}{N(n)}+C \cdot \sqrt{\frac{log(N(Parent(n))}{N(n)}}$$

• $U(n)$: Utility of node $n$ (number of wins)
• $N(n)$: Number of simulation involving $n$
• $Parent(n)$: Number of simulation involving the parent of $n$
• $C$: Exploration parameter

Exam questions

2018 02 22 Q3

Clarify the main ideas underlying Monte Carlo Tree Search (MCTS): explain what MCTS is, what it is used for, and describe its main features.